交易系统优选就是为特定的交易对象选择最佳的交易系统，从而增强对该交易对象实际操作的盈利性。人们从不同的角度，采用不同的技术方法建立了不同的交易系统，但是不同的交易系统运用于不同交易对象的交易结果是完全不同的，这就是不同的交易系统有着不同的适用性。

交易系统优选的原理就是:投资者选择列表中的相关交易系统(可以是部分，也可以是全部)对某一个对象进行交易系统检测，得出相关的评价结果。投资者可以选择相关评价项目的结果进行排序分析，确定该评价项目表现最佳的交易系统。

例如，为特定的交易对象华能国际(600011)进行交易系统优选。在交易系统列表中，选择了BIAS, KDJ, MA, KD, DMI, BOLL, CCI等交易系统作为优先对象。以日线为分析周期，以总收益最大化为测试目标，检测2003年2月6日至2004年2月10日期间内，交易x由象相对于各交易系统的盈利表现。结果显示:BIAS交易系统的目标收益为77.5%，年收益率为76.7%，排列在所有参加优选的交易系统之首(图5-3-10)。

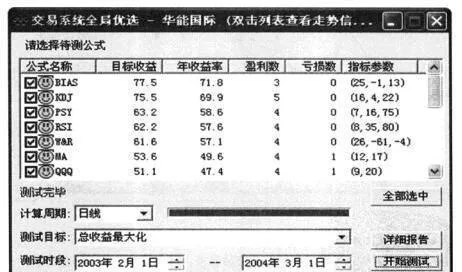
图5-3-10

由此可以得出，在这些交易系统中，BIAS交易系统相对于华能国际而言，是最佳的交易系统。

相关文章