停板機會確立
停板機會可分爲停板市場機會、停板波段機會和停板股性機會三種類型。
停板市場機會
停板的市場機會主要表現在以下兩個方面:
(1)市場的趨勢方向決定個股停板方向。
市場走勢決定個股走勢,市場方向決定個股方向,這是一個普遍性的市場規則。雖然有些個股逆市運行,但並不能改變這一市場規律的本質。具體表現爲:
1. 多頭市場個股選擇漲停板的機會較多。
2. 空頭市場個股選擇跌停板的機會較多。
(2)市場的趨勢強度決定了個股停板數量。
市場處於弱勢調整行情時,個股停板的機會較少。市場處於強勢運行行情時,個股停板的機會較多。個股大面積的漲跌停板是市場趨勢強勁的重要表現。比如,2004年1月8日,大盤展開了一輪強勁的多頭行情,當日表現尤其強勁,出現了個股大面積漲停板現象(圖2-7-2)。
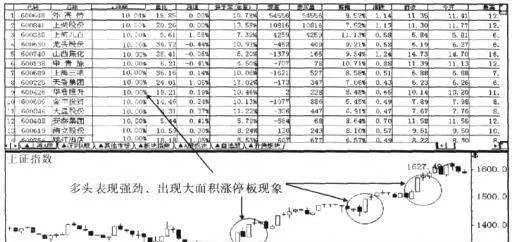
圖2-7-2
此外,板塊市場也是市場機會的表現形式之一,板塊聯動促成同一板塊個股同步走強。當板塊出現強勢運行態勢時,板塊內個股強勢漲跌停板的機會大大增加。
停板波段機會
就個股階段性趨勢運行而言,漲跌停板機會包含在趨勢運行的各個階段:
(1)趨勢啓動的停板機會。
趨勢啓動階段的停板通常是一輪行情啓動的重要信號。如有些個股經過長時間的弱勢整理,以突發性的漲停來啓動一輪新的趨勢行情。啓動階段的第一個停板機會具有突發性。通常難以預先把握。短線投資者通常可以通過趨勢結構分析和盤中短線分析進行實時跟進,把握部分機會。有些個股以開盤漲跌停啓動行情,此類機會無法把握。
啓動初期的停板如果盤中短線跟進,通常具有較好的安全性和收益性。啓動漲停後的次日個股往往會延續這種強勢。
(2)趨勢中途的停板機會。
趨勢中途主要是拉昇階段,停板機會相對最多,短線的收益率最大。超級強勢個股往往在拉昇階段出現連續停板的壯觀景象。拉昇階段應該是停板操作的黃金波段。
(3)趨勢末端的停板機會。
趨勢末端個股的表現不盡相同。有些個股在趨勢行情的末端作減速運行,表現爲高位弱勢震盪走勢;而有些個股則上演毀滅之前的最後瘋狂,出現強勢停板走勢。總體來說,趨勢末端的停板機會相對較少,並且風險性極大,有些個股甚至出現從漲停到跌停的巨大反差走勢。T+1交易制度下,追逐趨勢末端停板機會的風險極大。
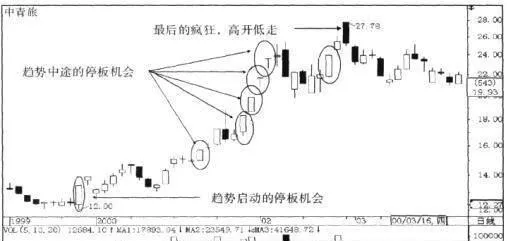
圖2-7-3
圖2-7-3顯示了中青旅(600138) 2000年1-2月間趨勢的強勢運行狀況。圖中顯示該股在多頭趨勢啓動,之初以一個低位漲停板發出趨勢啓動信號,隨後該股經過一浪盤升,二浪小幅調整,展開了強勢三浪快速拉昇,16個交易日漲停板數最達到5個。該股在五浪之後形成多頭頂部,完成一個漲停板的突破態勢。結果,該股上演多頭趨勢終結前的最後瘋狂:再次以漲停高開,隨即高開低走,結束了多頭趨勢。
停板股性機會
停板股性是研究停板市場機會的重要技術視角。在超級短線強勢機會中,我們深入地探討了強勢股股性重要的技術內涵:股性就是個股所表現出來的特有趨勢波動的個性。
超級短線強勢股股性的技術原則主要表現在兩個方面:
(1)歷史往往重演,強勢股的股性將在未來重複顯現。
(2)最相鄰的股性對當前走勢的影響最大。
強勢股股性的技術原則完全適用於停板股性的研究,因爲停板就是個股強勢股性極端的表現。
由此,可以推導出停板股性的技術原則:
(1)歷史往往重演,強勢漲跌停板的個股將在未來重現強勢停板的態勢。一隻曾經連續漲停的個股,往往在未來還會出現連續漲停的格局;一隻停板歷史表現較少的個股,往往在未來還會延續這種稀疏的停板走勢。
(2)最相鄰的停板態勢對最近的波段運行影響最大。這表現爲:同一波段如果出現連續停板的強勢格局,那麼這種強勢停板格局將在最相鄰的波段重複出現。圖2-7-4顯示了上海梅林(600073)強勢漲停板歷史股性重演的格局。
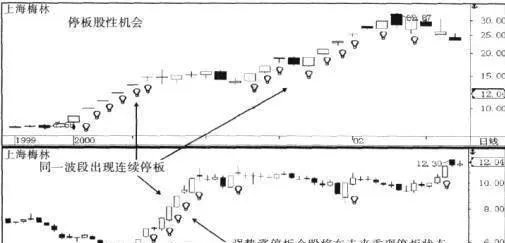
圖2-7-4
2000年1月,該股爆發了一輪強勁的多頭行情,在第一多頭攻擊波中,出現了連續8個漲停板;在第三多頭攻擊波中,出現了連續10個漲停板。該股經過三年的整理,於2003年11月13日再次姍發強勁的多頭行情,在第一多頭攻擊波中,出現了連續5個漲停板,充分體現了強勢漲停板歷史股性重演的市場特性。
停板技術誤區
漲跌停板的技術研究是超級短線技術最熱門的話題,這是由於漲跌停板可觀的投資效率和效益,給短線投資者帶來了巨大的心理震撼和衝擊。
在數量衆多的短線技術理論中,對漲跌停板的研究總是能夠吸引短線投資者的目光,不僅如此,幾乎所有的短線投資者都將漲跌停板相關技術視爲最有價值的短線技術。然而,對停板技術的研究存在着許多誤區,縱觀當今有關漲跌停板的技術理論,停板誤區的技術表現尤其明顯。這主要表現在以下幾個方面:
(1)孤立地、片面地研究漲跌停板。
漲跌停板是一個特定的市場現象,其木身是趨勢發展變化的必然結果,是市場歷史趨勢的延續。諸多漲跌停板技術理論僅僅以實時盤中漲跌停板態勢爲着眼點,機械地、孤立地研究漲跌停板現象,而不是歷史地、完整地研究漲跌停板的市場內涵和技術內涵。
(2)以漲跌停板的市場結果來求證漲跌停板的原因。
從本質上說,漲跌停板是一個不確定的市場現象。我們可以通過相關分析和研判,有效地確定趨勢的強度,但強到何種程度,是否強到非漲跌停板不可,沒有人能夠給出精確的結論。一隻低位強勢漲停的股票,通常次日會延續強勢的趨勢運動,可以表現爲連續漲停,也可以不以漲停報收,這些都是漲跌停板的市場不確定性。漲跌停板只是趨
勢運動的結果,絕不可用結果來求證漲跌停板的原因。那些以漲跌停板的結果說明漲跌停板本身的所謂,停板技術”,都屬於馬後炮式的僞技術理論,根本沒有實戰操作性。
(3)機械地羅列漲跌停板形態,沒有任何技術內涵。
漲跌停板在實時盤中會有多種表現形式,並可歸納爲多種停板形態。但是,停板形態本身並不重要,重要的是停板形態所蘊含的實戰技術內涵。機械地羅列漲跌停板形態,並冠以各種名頭,都是沒有意義的。
(4)停板技術理論和實戰交易相脫離。
研究技術理論的最終目的是爲了實戰交易,然而諸多停板技術理論與實戰交易嚴重脫鉤,有些理論根本沒有可操作性。比如,某一停板技術理論研究個股如何從跌停板到漲停板,並在一張從跌停板到漲停板的趨勢圖中標明短線進場位。其實,這完全是一個馬後炮式的僞技術理論,試想,如果在跌停板打開瞬間短線進場,能確保一定會漲停板嗎?這完全是用從跌停板到漲停板的市場結果,來想象“最佳停板交易”過程。