什麼是鐘形曲線?
鐘形曲線是一種常見的變量分佈類型,也稱爲正態分佈。“鐘形曲線”一詞源於用於描述正態分佈的圖形由對稱的鐘形曲線組成。
曲線的最高點,或者說鐘形曲線的頂部,代表一系列數據中最可能發生的事件(在本例中是平均值、衆數和中位數),而所有其他可能發生的事件則對稱分佈在平均值周圍,在峯的兩側形成一條向下傾斜的曲線。鐘形曲線的寬度用其標準差來描述。
關鍵點
- 鐘形曲線是描述正態分佈的圖形,其形狀類似於鐘形。
- 曲線頂部顯示所收集數據的平均值、衆數和中位數。
- 其標準差描述了鐘形曲線相對於平均值的相對寬度。
- 鐘形曲線(正態分佈)在統計學中被廣泛使用,包括分析經濟和金融數據。
理解鐘形曲線
“鐘形曲線”一詞用於描述正態概率分佈的圖形描述,其與平均值的底層標準差構成了彎曲的鐘形曲線。標準差是一種度量,用於量化一組給定值在平均值附近的數據離散度的變異性。平均值是指數據集或序列中所有數據點的平均值,位於鐘形曲線的最高點。
金融分析師和投資者在分析證券收益或整體市場敏感度時,通常使用正態概率分佈。在金融領域,描述證券收益的標準差被稱爲波動率。
例如,呈現鐘形曲線的股票通常是藍籌股,波動性較低,行爲模式更可預測。投資者使用股票過去收益的正態概率分佈來預測未來的預期收益。
除了教師在比較考試成績時使用鐘形曲線外,鐘形曲線在統計學領域也得到廣泛應用。鐘形曲線有時也用於績效管理,將工作表現平均的員工置於圖表的正態分佈中。高績效員工和低績效員工分別位於斜率下降的兩側。對於大型公司進行績效評估或制定管理決策時,鐘形曲線非常有用。
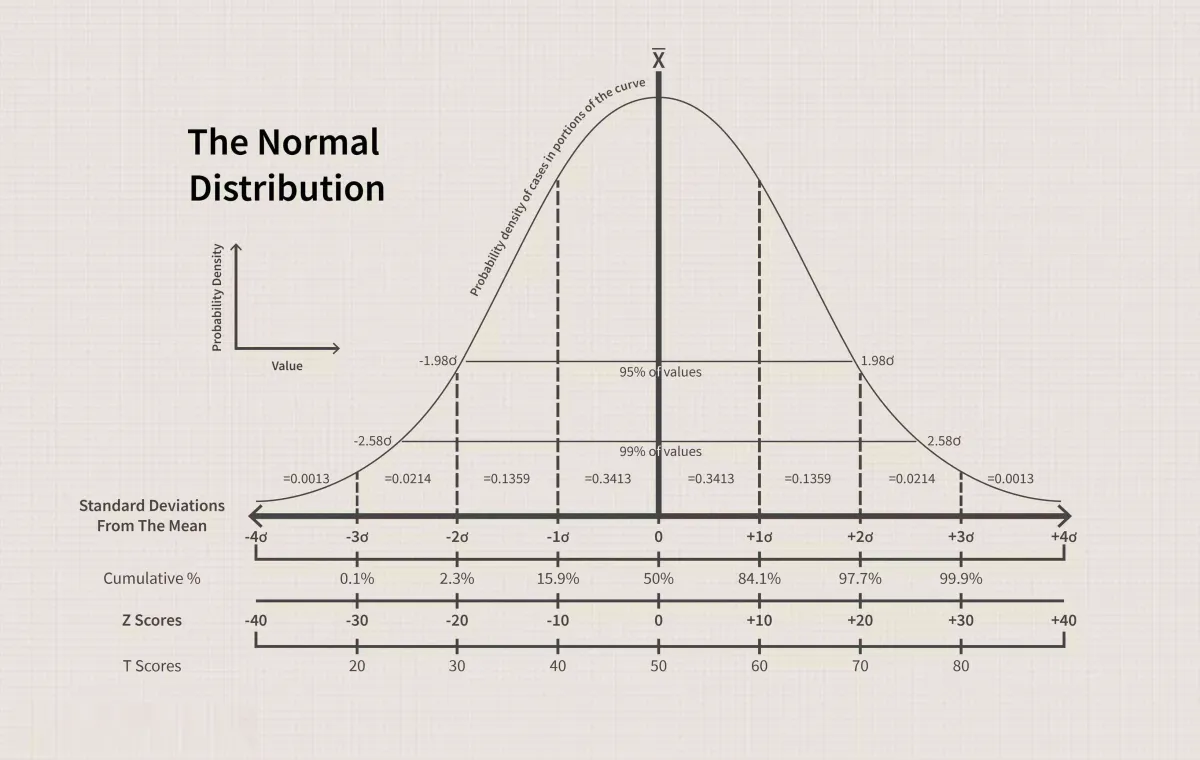
鐘形曲線示例
鐘形曲線的寬度由其標準差定義,標準差計算爲樣本中數據圍繞均值的變化程度。例如,使用經驗法則,如果收集100個測試分數並將其用於正態概率分佈,則其中68%的測試分數應在均值上下一個標準差的範圍內。偏離均值兩個標準差的範圍內應包含收集到的100個測試分數中的95%。偏離均值三個標準差的範圍內應包含99.7%的分數(見上圖)。
測試分數如果爲極端異常值(例如 100 分或 0 分),則會被視爲長尾數據點,因此正好位於三個標準差範圍之外。
鐘形曲線與非正態分佈
然而,正態概率分佈假設在金融領域並不總是成立。股票和其他證券有時會呈現出非正態分佈,不再像鐘形曲線。
非正態分佈的尾部比鐘形曲線(正態概率)分佈更肥厚。肥厚的尾部會向投資者發出負面信號,表明出現負收益的概率更大。
鐘形曲線的侷限性
使用鐘形曲線對績效進行評分或評估會強制將人羣分爲較差、中等或較好三類。對於較小的羣體,必須將一定數量的人分入每個類別以擬合鐘形曲線,這會對這些個人造成傷害。有時,他們可能都是中等甚至較好的工人或學生,但考慮到需要將他們的評級或成績擬合到鐘形曲線,一些人被迫歸入較差組。實際上,數據並不完全正態。有時,均值上下之間存在偏度或缺乏對稱性。有時還會出現厚尾(峯度過高),使尾部事件發生的可能性高於正態分佈的預測值。
鐘形曲線有哪些特徵?
鐘形曲線是以所有被測數據點的平均值爲中心的對稱曲線。鐘形曲線的寬度由標準差決定——68% 的數據點位於平均值的一個標準差範圍內,95% 的數據點位於平均值的兩個標準差範圍內,99.7% 的數據點位於平均值的三個標準差範圍內。
鐘形曲線在金融中如何應用?
分析師在對與投資相關的各種潛在結果進行建模時,通常會使用鐘形曲線和其他統計分佈。根據所進行的分析,這些結果可能包括未來股價、未來盈利增長率、潛在違約率或其他重要現象。在分析中使用鐘形曲線之前,投資者應仔細考慮所研究的結果是否符合正態分佈。否則,可能會嚴重損害最終模型的準確性。
鐘形曲線的侷限性是什麼?
儘管鐘形曲線是一個非常有用的統計概念,但它在金融領域的應用卻受到限制,因爲金融現象(例如預期股市收益)並不完全符合正態分佈。因此,在預測這些事件時過度依賴鐘形曲線可能會導致不可靠的結果。儘管大多數分析師都很清楚這一侷限性,但克服這一缺陷相對困難,因爲通常不清楚應該使用哪種統計分佈作爲替代。