什么是钟形曲线?
钟形曲线是一种常见的变量分布类型,也称为正态分布。“钟形曲线”一词源于用于描述正态分布的图形由对称的钟形曲线组成。
曲线的最高点,或者说钟形曲线的顶部,代表一系列数据中最可能发生的事件(在本例中是平均值、众数和中位数),而所有其他可能发生的事件则对称分布在平均值周围,在峰的两侧形成一条向下倾斜的曲线。钟形曲线的宽度用其标准差来描述。
概要
- 钟形曲线是描述正态分布的图形,其形状类似于钟形。
- 曲线顶部显示所收集数据的平均值、众数和中位数。
- 其标准差描述了钟形曲线相对于平均值的相对宽度。
- 钟形曲线(正态分布)在统计学中被广泛使用,包括分析经济和金融数据。
理解钟形曲线
“钟形曲线”一词用于描述正态概率分布的图形描述,其与平均值的底层标准差构成了弯曲的钟形曲线。标准差是一种度量,用于量化一组给定值在平均值附近的数据离散度的变异性。平均值是指数据集或序列中所有数据点的平均值,位于钟形曲线的最高点。
金融分析师和投资者在分析证券收益或整体市场敏感度时,通常使用正态概率分布。在金融领域,描述证券收益的标准差被称为波动率。
例如,呈现钟形曲线的股票通常是蓝筹股,波动性较低,行为模式更可预测。投资者使用股票过去收益的正态概率分布来预测未来的预期收益。
除了教师在比较考试成绩时使用钟形曲线外,钟形曲线在统计学领域也得到广泛应用。钟形曲线有时也用于绩效管理,将工作表现平均的员工置于图表的正态分布中。高绩效员工和低绩效员工分别位于斜率下降的两侧。对于大型公司进行绩效评估或制定管理决策时,钟形曲线非常有用。
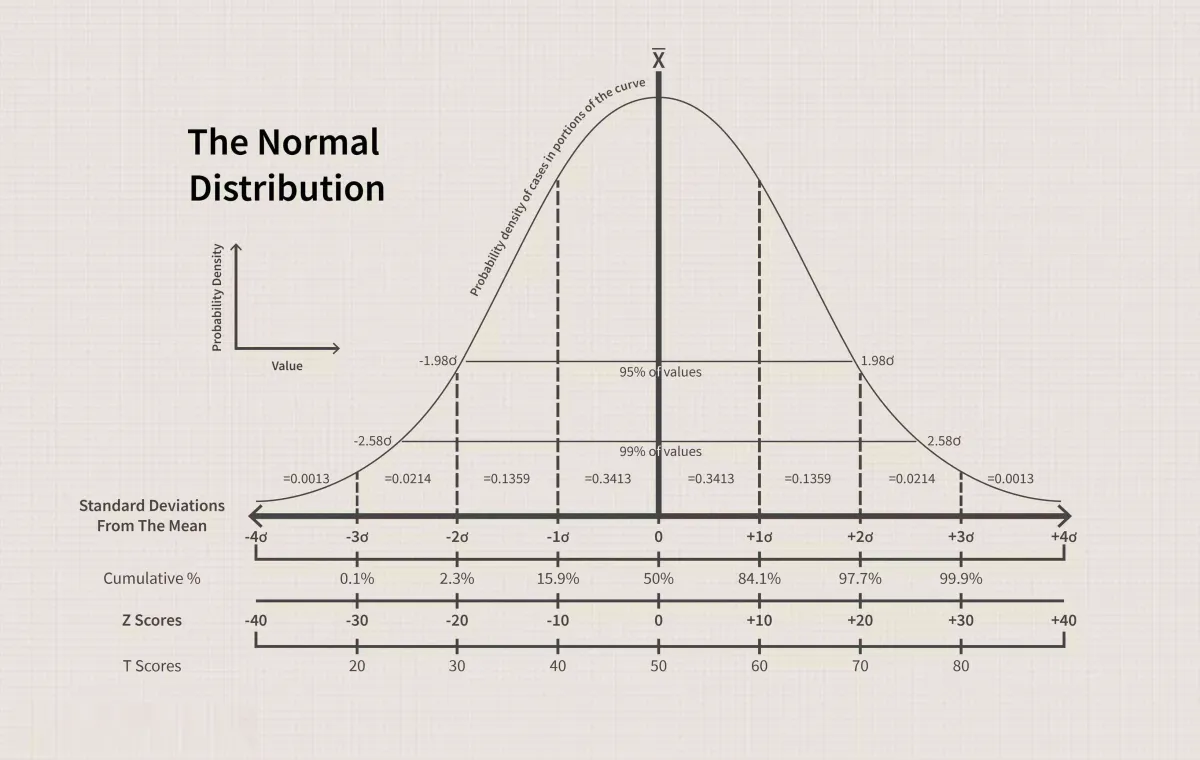
钟形曲线示例
钟形曲线的宽度由其标准差定义,标准差计算为样本中数据围绕均值的变化程度。例如,使用经验法则,如果收集100个测试分数并将其用于正态概率分布,则其中68%的测试分数应在均值上下一个标准差的范围内。偏离均值两个标准差的范围内应包含收集到的100个测试分数中的95%。偏离均值三个标准差的范围内应包含99.7%的分数(见上图)。
测试分数如果为极端异常值(例如 100 分或 0 分),则会被视为长尾数据点,因此正好位于三个标准差范围之外。
钟形曲线与非正态分布
然而,正态概率分布假设在金融领域并不总是成立。股票和其他证券有时会呈现出非正态分布,不再像钟形曲线。
非正态分布的尾部比钟形曲线(正态概率)分布更肥厚。肥厚的尾部会向投资者发出负面信号,表明出现负收益的概率更大。
钟形曲线的局限性
使用钟形曲线对绩效进行评分或评估会强制将人群分为较差、中等或较好三类。对于较小的群体,必须将一定数量的人分入每个类别以拟合钟形曲线,这会对这些个人造成伤害。有时,他们可能都是中等甚至较好的工人或学生,但考虑到需要将他们的评级或成绩拟合到钟形曲线,一些人被迫归入较差组。实际上,数据并不完全正态。有时,均值上下之间存在偏度或缺乏对称性。有时还会出现厚尾(峰度过高),使尾部事件发生的可能性高于正态分布的预测值。
钟形曲线有哪些特征?
钟形曲线是以所有被测数据点的平均值为中心的对称曲线。钟形曲线的宽度由标准差决定——68% 的数据点位于平均值的一个标准差范围内,95% 的数据点位于平均值的两个标准差范围内,99.7% 的数据点位于平均值的三个标准差范围内。
钟形曲线在金融中如何应用?
分析师在对与投资相关的各种潜在结果进行建模时,通常会使用钟形曲线和其他统计分布。根据所进行的分析,这些结果可能包括未来股价、未来盈利增长率、潜在违约率或其他重要现象。在分析中使用钟形曲线之前,投资者应仔细考虑所研究的结果是否符合正态分布。否则,可能会严重损害最终模型的准确性。
钟形曲线的局限性是什么?
尽管钟形曲线是一个非常有用的统计概念,但它在金融领域的应用却受到限制,因为金融现象(例如预期股市收益)并不完全符合正态分布。因此,在预测这些事件时过度依赖钟形曲线可能会导致不可靠的结果。尽管大多数分析师都很清楚这一局限性,但克服这一缺陷相对困难,因为通常不清楚应该使用哪种统计分布作为替代。