我們將通過深赤灣(000022)的趨勢結構分析,展示均衡和非均衡平衡狀態的結構分析方法(圖1-4-29)。
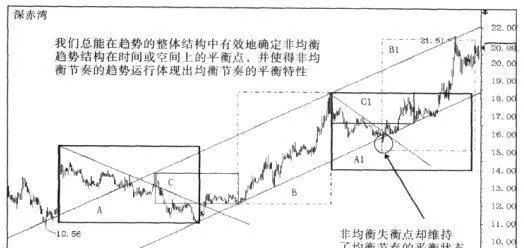
圖1-4-29
(1)局部的、微觀的非均衡平衡狀態,整體的、宏觀的均衡平衡狀態。
在平衡矩形A和Al等相關的調整和減速波段中,該股的回調波段呈現一種弱勢趨勢狀態,顯示出趨勢的非均衡節奏;價格在調整波段呈現出不規則的波動狀態。同時,在總體的趨勢結構中,趨勢卻顯示了均衡節奏的平衡狀態,即A與Al的時間平衡,C與Cl的時間平衡,B與B1的價格平衡。
(2)非均衡平衡的失衡並不愈味着整體趨勢結構的失衡。
在Al的價格運動區域,價格跌破了上升趨勢線,表現出非均衡趨勢的失衡狀態,但運用雙波法則對兩個調整波進行比對,結果顯示:當前非均衡狀態的平衡並沒有超越矩形A的調整幅度,顯示了該趨勢的有效性。當調整的時間達到C與C1的平衡時,該股再度上攻,延續着原趨勢的運行。
(3)非均衡節奏平衡與均衡節奏平衡的高度重合。
當均衡節奏平衡狀態與非均衡節奏的平衡狀態相一致時,是對趨勢方向的平衡狀態強有力的確認。圖中顯示:價格在B與B1的平衡矩形中實現了平衡,同時,在均衡節奏的價格平衡處同步形成上升通道上軌的平衡。此外,價格平衡處也與上升頂部趨勢線處於高度的平衡狀態。
需要指出的是,圖中的非均衡與均衡平衡狀態的高度一致,也是週期共振的重要表現。