個股輪動戰法之三
戰法描述
在板塊行情中,輪動股往往只出現在少數幾個強勢股中。表現爲:股輪漲的領漲股通常僅出現在少數幾個板塊強勢股中;通常僅出現在少數幾個板塊弱勢股中。在多頭市場,個在空頭市場,個股輪跌的領跌股
戰法要點
(1)在多頭市場,個股多頭板塊輪動通常在階段性強勢排名靠前的個股中展開。對階段性前幾名的個股應予以密切關注,這類個股將顯示“強者恆強”的市場特性,松蕃領漲板塊。
(2)在空頭市場,個股多頭板塊輪動通常在階段性弱勢排名靠前的個股中展開。對階段性弱勢前幾名的個股應予以密切關注,這類股將顯示“弱者恆弱”的市場特性,輪番領跌板塊。
(3)在多頭市場,板塊階段強勢股應作爲重點對象予以高度關注。當板塊走強,該股出現調整,是買入時機,因爲今天的調整是爲明天的領漲所作的準備。
(4)在空頭市場,板塊階段弱勢股應作爲重點對象予以高度關注。當板塊走弱,該股出現反彈,是被套投資者最佳的逃命時機,因爲今天的反彈是爲明天的大跌所做的預謀。
戰法案例
2003年26月間汽車板塊的強勢上升行情中,板塊內個股強勢上漲,其中長安汽車、江鈴汽車、上海汽車、一汽轎車等幾個板塊強勢股輪番引領發動當日的上漲行情。這就要求對板塊行情的操作中鎖定板塊內少數幾個輪動性最好的強勢股,這是板塊操作利潤最大化、風險最小化的有效策略(圖4-4-3)。
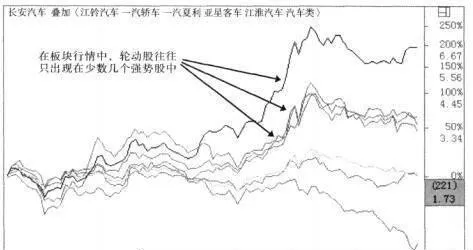
圖4-4-3