战法38破档三阳收十字
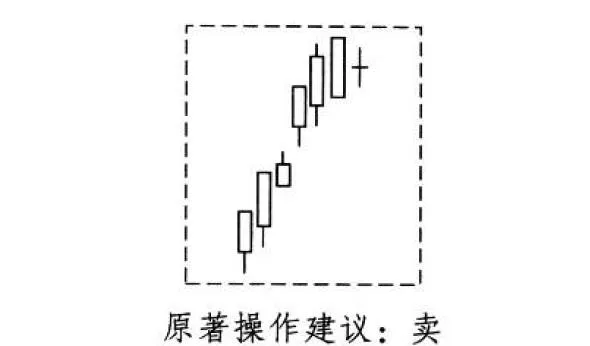
原著注解:
在破档朝上连出三支阳线后。第四天突然冒出十字星,此为多头抛售的良机。因为在十字星出现后可能迅速回补前空,再者在一连串上升的走势中连出六支阳线,也容易引发高价份戒而回落。十字星后翌日如再开低,很可能会引发多头大抛售而令行市崩溃。
对于破档三阳收十字线,笔者基本上认同原著的观点,投资者可以以卖出为主。但是,笔者通过大量实战图形观察,发现并不一定都是卖,很多图形出现了破档三阳收十字线后,虽然有调整,但调整的幅度很小,然后又继续上升了,投资者卖出该股后,就很难找到低位回补的机会了。因此,投资者必须要根据实战形态来进行分析。
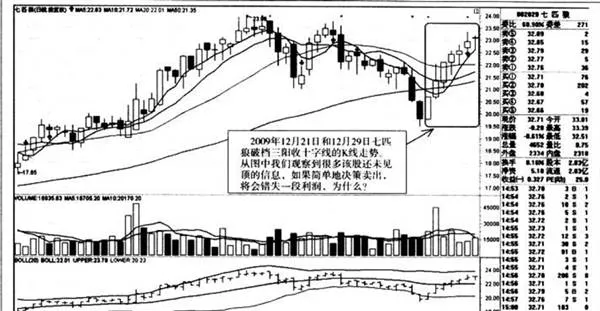
上图为2009年12月21日和12月29日七匹狼破档三阳收十字线的K线走势。从图中我们观察到很多该股还未见顶的信息,如果简单地决策卖出,将会错失一段利润,为什么?
第一,布林通道还未见顶。
第二,成交量有温和放大的迹象。
第三,连续两波的急跌,又重新拉回高位让你解套,后市必定不止现在的价钱。笔者认为可继续持股。
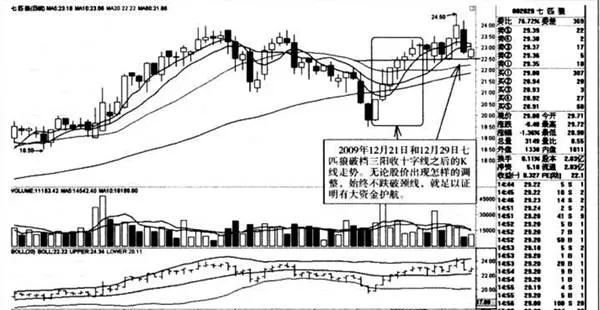
上图为2009年12月21日和12月29日七匹狼破档三阳收十字线之后的K线走势。无论股价出现怎样的调整,始终不跌破颈线,就足以证明有大资金护航。
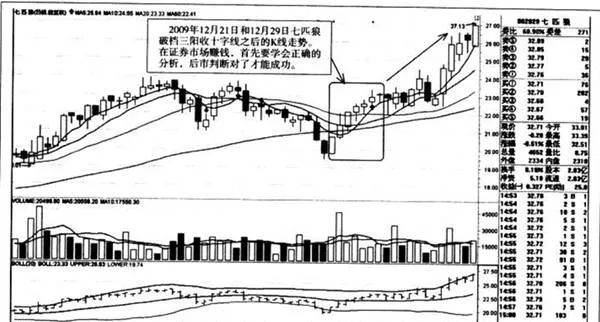
上图为2009年12月21日和12月29日七匹狼破档三阳收十字线之后的K线走势。从图中我们看到该股虽然出现了调整,但是,其调整的幅度却非常小。因此,在证券市场上赚钱,首先要学会正确的分析,后市判断对了才能成功。
总结本章要点,笔者认为,对于破档三阳收十字线,投资者可以按原著的要求先以卖出为主。但是,投资者脑海里要注意一点,就是要提防主力反技术操作这一招。